Are you tired of staring at a page full of complex equations, feeling overwhelmed and unsure where to even begin? Well, what if I told you that the simple act of sketching could help unlock the secrets hidden within those daunting mathematical mysteries? That’s right! Sketching functions and graphics can be an incredibly powerful tool for solving equations. Not only does it allow us to visualize mathematical concepts with ease, but it also provides a step-by-step guide towards finding solutions. So grab your pencil and join me on this journey as we explore how sketching can revolutionize the way we solve equations. Get ready to unleash your inner artist and mathematician all at once!
The Benefits of Sketching in Mathematics
When it comes to mathematics, the benefits of sketching are endless. One of the key advantages is that it allows us to visually grasp complex concepts and relationships. Instead of getting lost in a sea of numbers and symbols, sketching brings equations and functions to life on paper.
By putting pen to paper, we can observe patterns, identify trends, and make connections that might not be immediately apparent from just looking at an equation alone. Sketching helps us see the bigger picture and understand how different elements interact with each other.
Another benefit of sketching is its ability to enhance problem-solving skills. When faced with a challenging equation, taking the time to draw out its graph or function can provide valuable insights into possible solutions. It allows us to break down problems into smaller components, making them more manageable and easier to approach.
Furthermore, sketching encourages creativity in problem-solving. It empowers us to think outside the box and consider alternative approaches when traditional methods fail. By visualizing equations through sketches, we open ourselves up to new possibilities and unconventional strategies for finding solutions.
Not only does sketching help improve our understanding of mathematical concepts but it also aids in retention. When we actively engage with math by drawing diagrams or graphs, we create mental associations that strengthen our memory recall later on.
So next time you find yourself faced with a daunting equation or concept in mathematics, remember the power of your pencil! Embrace your inner artist-mathematician hybrid and let sketching guide you toward unlocking those elusive solutions.
Understanding Functions and Graphics
As a fundamental concept in mathematics, understanding functions and graphics is essential for solving equations. Functions are mathematical relationships between two variables, often represented by an equation or formula. Graphics, on the other hand, involve visual representations of these functions using graphs.
By sketching functions and graphics, we can better understand their behavior and properties. By examining the shape of a graph or analyzing key points on a curve, we can gain valuable insights about the underlying function.

Graphs provide us with a visual representation of how different variables interact within an equation. They allow us to see patterns and trends and even identify critical points such as zeros or intercepts. This information becomes invaluable when it comes to solving equations, as it helps guide our decision-making process.
Sketching functions and graphics is not only visually appealing but also provides practical benefits for equation solving. It allows us to visualize complex concepts more easily and aids in identifying solutions that may not be immediately apparent from looking at algebraic expressions alone.
By following a step-by-step approach to sketching functions and graphics in relation to equations, we can systematically analyze various aspects, such as domain restrictions or asymptotes, that impact the solution space. This systematic process enhances our problem-solving abilities by providing additional tools for tackling challenging equations.
Let’s take an example: suppose we have an equation y = 2x + 3. By sketching this linear function on graph paper with labeled axes, we can quickly determine its slope (2) and y-intercept (3). Armed with this knowledge, we’re equipped to solve related problems like finding x-values where y = 0 or evaluating inequalities involving this function.
It’s important to note that while sketching is helpful in solving many types of equations, it should not replace formal mathematical techniques entirely. When necessary, rigorous analysis through algebraic manipulation must go along with sketches to provide guidance.
The Role of Sketching in Solving Equations
Sketching plays a crucial role in solving equations, allowing us to visualize the behavior and relationships between variables. By graphing functions, we can gain valuable insights into their properties and make informed decisions when solving equations.
When faced with an equation, sketching helps us understand the nature of the problem. It allows us to see how different parts of the equation interact and provides clues on where solutions may lie. By visually representing the equation through graphs, we can analyze its behavior as well as identify key points such as intercepts, maxima, or minima.
Through the use of sketching functions and graphics for equation solving, we can break down complex problems into simpler components. This process not only simplifies our understanding but also highlights patterns or trends that may be hidden within the equation itself.
By observing the shape of a function’s graph, we can often deduce important information about its solutions. For instance, if two graphs intersect at a certain point on a coordinate plane, it signifies that these x and y values satisfy both equations simultaneously, thus providing possible solutions.
Moreover, by examining how curves change direction or steepness around critical points like inflection points or turning points (where derivatives equal zero), sketching enables us to identify potential solution intervals more effectively. These visual representations guide our problem-solving strategies towards efficient methods such as factoring or applying specific algebraic techniques.
Sketching is an invaluable tool when it comes to solving equations. Its ability to provide visual cues allows us to grasp complex concepts more easily while aiding in identifying solution intervals and making educated decisions throughout the problem-solving process.
Step-by-Step Guide to Sketching Functions and Graphics for Equation Solving
One effective method for solving equations is by sketching functions and graphics. This step-by-step guide will show you how to use this technique to your advantage.
- Understand the equation: Before you begin sketching, make sure you clearly understand the equation you need to solve. Identify any key variables or constants involved.
- Plot key points: Start by plotting key points on your coordinate plane. These points can be obtained by substituting different values of x into the equation and solving for y. Choose a range of values that will give you a good sense of the shape of the function.
- Determine end behaviors: Next, determine the end behaviors of the function as x approaches positive infinity and negative infinity. Does it approach a specific value or go off in different directions?
- Sketch the curve: Using your plotted points and knowledge about end behavior, sketch a smooth curve that represents the function’s graph on your coordinate plane.
- Find intersections with other functions or lines: If there are other functions or lines involved in your problem, find their intersections with your graph using algebraic methods such as substitution or elimination.
- Analyze intersections: Analyze these intersections to find possible solutions to your equation(s). Pay attention to where two curves cross each other and if they intersect at specific coordinates.
- Check solutions algebraically: Once you have potential solutions, check them algebraically by plugging them back into the original equation(s) and verifying if they satisfy all conditions.
By following this step-by-step guide, sketching functions and graphics can significantly aid in solving equations effectively!
Examples of Using Sketching to Solve Equations
As mentioned earlier, sketching can be a powerful tool for solving equations. Let’s take a look at some examples to see how it works in practice.
Consider the equation y = 2x + 3. By sketching the graph of this equation on a coordinate plane, we can easily determine its solutions. The graph is a straight line with a slope of 2 and a y-intercept of 3. We can visually see that any point on this line satisfies the equation.
Now, let’s tackle a quadratic equation: x^2 – 4x + 4 =0. By sketching the corresponding parabola, we can find its solutions as well. In this case, the parabola opens upward and intersects the x-axis at only one point (x = 2). By symmetry, we know that there must be another solution at x=2 as well.

Moving on to trigonometric functions, consider the equation sin(x) = cos(π/4). By sketching their respective graphs on separate axes and analyzing their intersection points, we can determine where they are equal to each other.
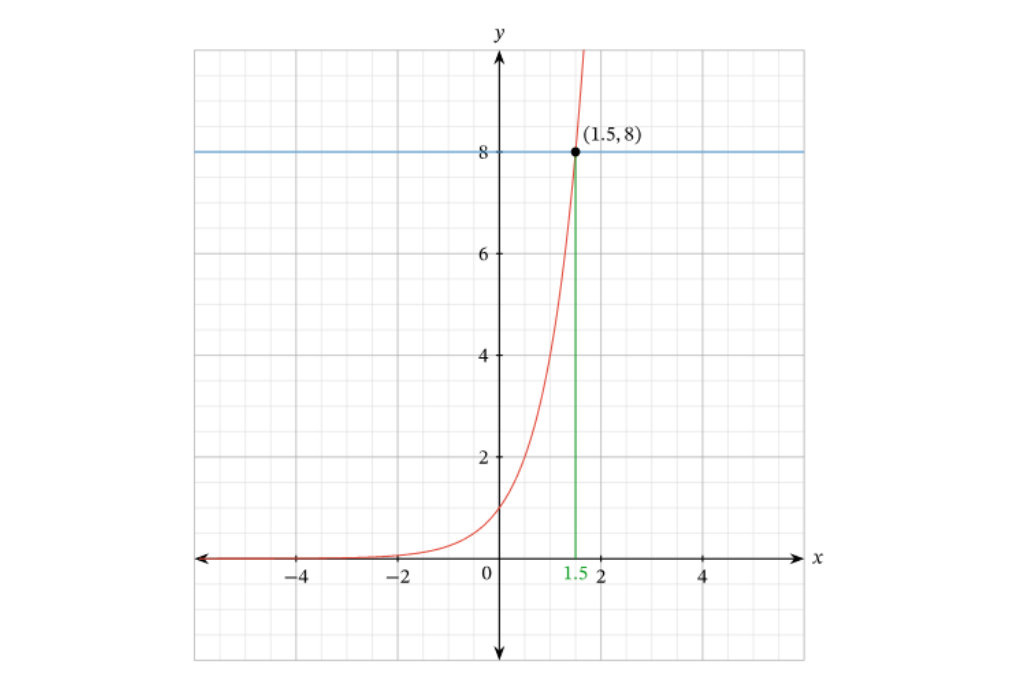
Sketching also helps when dealing with exponential equations like e^x = 5 or logarithmic equations like log(x) = log(1000). Sketching their graphs allows us to identify their intersecting points and find solutions effortlessly.
In conclusion, oops! Sorry about that slip-up! I hope these examples have shown you just how useful sketching functions and graphics can be when it comes to solving equations effectively. So next time you’re faced with an equation puzzle, grab your pen and paper because sometimes all it takes is a simple sketch to unlock the solution!
Common Mistakes to Avoid When Using Sketching for Equation Solving
While sketching functions and graphics can be a powerful tool for solving equations, it’s important to be aware of some common mistakes that students often make. By avoiding these pitfalls, you can ensure that your sketches are accurate and effective in helping you find solutions to equations.
- Neglecting the domain: One mistake many students make is not considering the domain of the function before sketching its graph. It’s crucial to understand any restrictions on x-values or vertical asymptotes, as this will impact the shape and behavior of the graph.
- Misidentifying intercepts: Another common error is incorrectly identifying intercepts. When plotting points on the graph, it’s essential to double-check whether they intersect with axes at specific values or if they merely cross through them without touching.
- Ignoring symmetry: Many graphs exhibit symmetry either across the x-axis (even), y-axis (odd), or origin (neither). Failing to recognize these symmetrical properties can lead to incorrect sketches and potentially inaccurate equation solutions.
- Overlooking critical points: Critical points such as local maxima/minima or inflection points play a significant role in determining how an equation behaves locally. Neglecting these crucial locations on your graph may result in missing potential solution values.
- Inadequate labeling: A poorly labeled graph can lead to confusion when attempting to solve equations using sketching methods. Ensure that all axis labels, tick marks, and coordinates are clearly marked so that you can accurately read off values from your sketch during analysis.
By being mindful of these common mistakes and taking steps towards precision in your sketches, you’ll enhance your ability to solve equations effectively using visual representations of functions and graphics.
Continue practicing sketching techniques and honing your skills over time, incorporating feedback from teachers or peers if possible. Remember that practice makes perfect when it comes to mastering the art of sketching functions and graphics for equation solving.
Honing your sketching abilities for equation solving is paramount to mastery, and How Live Online Classes Have Changed The Way Of Education. Incorporate emerging educational methods by taking advantage of online resources and soliciting feedback from instructors or peers during practice sessions. By doing this, not only will your sketching techniques improve, but you’ll also adapt more fully to the ever-evolving landscape of education, guaranteeing an efficient learning experience. Remember, the journey toward sketching perfection involves adopting innovative educational approaches!




